
SL Paper 3
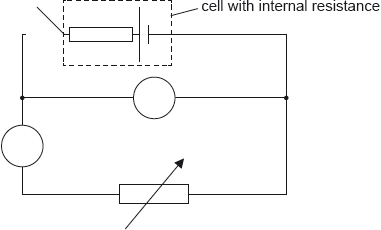
The circuit shown may be used to measure the internal resistance of a cell.
The ammeter used in the experiment in (b) is an analogue meter. The student takes measurements without checking for a “zero error” on the ammeter.
An ammeter and a voltmeter are connected in the circuit. Label the ammeter with the letter A and the voltmeter with the letter V.
In one experiment a student obtains the following graph showing the variation with current I of the potential difference V across the cell.

Using the graph, determine the best estimate of the internal resistance of the cell.
State what is meant by a zero error.
After taking measurements the student observes that the ammeter has a positive zero error. Explain what effect, if any, this zero error will have on the calculated value of the internal resistance in (b).
Markscheme
correct labelling of both instruments
[1 mark]
V = E – Ir
large triangle to find gradient and correct read-offs from the line
OR
use of intercept E = 1.5 V and another correct data point
internal resistance = 0.60 Ω
For MP1 – do not award if only \(R = \frac{V}{I}\) is used.
For MP2 points at least 1A apart must be used.
For MP3 accept final answers in the range of 0.55 Ω to 0.65 Ω.
[3 marks]
a non-zero reading when a zero reading is expected/no current is flowing
OR
a calibration error
OWTTE
Do not accept just “systematic error”.
[1 mark]
the error causes «all» measurements to be high/different/incorrect
effect on calculations/gradient will cancel out
OR
effect is that value for r is unchanged
Award [1 max] for statement of “no effect” without valid argument.
OWTTE
[2 marks]
Examiners report
An electrical circuit is used during an experiment to measure the current I in a variable resistor of resistance R. The emf of the cell is e and the cell has an internal resistance r.
A graph shows the variation of \(\frac{1}{I}\) with R.
Show that the gradient of the graph is equal to \(\frac{1}{e}\).
State the value of the intercept on the R axis.
Markscheme
«ε = IR + Ir»
\(\frac{1}{I} = \frac{R}{\varepsilon } + \frac{r}{\varepsilon }\)
identifies equation with y = mx + c
«hence m = \(\frac{1}{\varepsilon }\)»
No mark for stating data booklet equation
Do not accept working where r is ignored or ε = IR is used
OWTTE
«–» r
Allow answer in words